This article is the first one in the Random DS/Algo series. The purpose of this series is to just act as random collection of DS/Algo problems I solved so that in future I might revisit what I explained to people on the Internet 🤷♂️.
This is one those questions that I always practice before an interview.

The leetcode problem statement goes like this :-
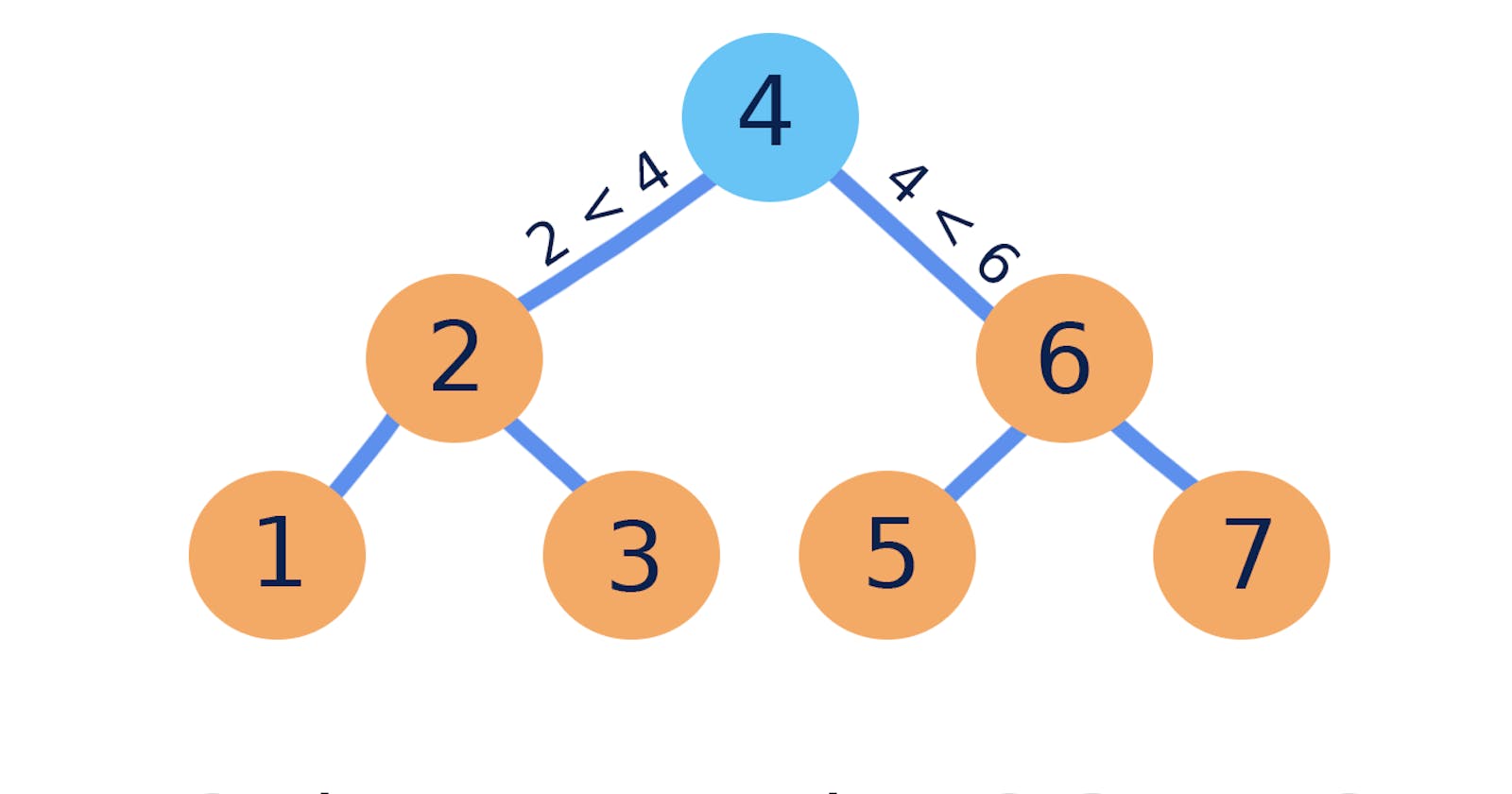
Given the root of a binary tree, determine if it is a valid binary search tree (BST). A valid BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.
There are 3 implementations that I know which can help us validate a BST.

Inorder traversal with extra space
One of the clean features of a BST is that if you do an inorder traversal of the same, you get the node values in a sorted order.
function isValidBST(root){
const arr = [];
helper(root,arr);
for(let index = 0;index<arr.length-1;index++){
if(arr[index+1]<=arr[index]){
return false;
}
}
return true;
}
function helper(root,arr){
if(!root)
return;
helper(root.left,arr);
arr.push(root.val);
helper(root.right,arr);
}
Approach breakdown :-
Initialize an empty array
arr.Call
helper(root,arr)which internally does :-Traverse the BST in inorder fashion.
Push each
root.valinside thearr.
Then we loop over the
arrand for any index if an element is less than or equal to previous element, then we simply returnfalse. This is because elements should have been strictly increasing as per the requirements.Otherwise, we return
true.

Inorder traversal without extra space
It's possible to do the above and exit early if there is an invalid BST without using extra arr space.
var isValidBST = function(root){
const prev = helper(root,null);
return prev.isNotValid ? false : true;
}
function helper(root,prev){
if(!root)
return prev;
prev = helper(root.left,prev);
if(prev && root.val <= prev.val){
prev.isNotValid = true;
}
if(prev?.isNotValid)
return prev;
prev = root;
prev = helper(root.right,prev);
return prev;
}
Approach breakdown :-
Let's consider
helper(root,prev)first (prevrepresents previous node) :-if(!root) return prev- If therootisundefined, we return theprevelement.prev = helper(root.left,prev)- We will first go through the left subtree for eachrootto find theprevelement.if(prev && root.val <= prev.val){ prev.isNotValid = true; }- Once we return from the left subtree , ifprevexists, we compareroot.valandprev.valto check if currentroot.valis less than or equal toprev.val. If it is, we create a property onprevby the name ofisNotValidand set it totrue.if(prev?.isNotValid) return prev;- Next we check if thisprev.isNotValidexists or not and if it does then we simply returnprevto exit early and not further proceed for subsequent right subtree.prev = root- This is how we set theprevvalue torootso that for next node we can use thisprevvalue for necessary comparisons.prev = helper(root.right,prev);- Going through the right subtree for eachrootto find theprevelement.return prev;- It's essential to return theprevto the calling function for value to reflect.
const prev = helper(root,null);- InsideisValidBST, we get theprevelement fromhelper(root,null).return prev.isNotValid ? false : true;- Ifprev.isNotValidexists then that means the BST is invalid and we returnfalseelse we returntrue.

Utilizing the BST property
In BST we can say that each node value will be more than it's left ancestor and less than it's right ancestor for it to be valid. This is what we are going to use now :-
var isValidBST = function(root){
return helper(root,-Infinity,Infinity);
}
function helper(root,leftMax,rightMax){
if(!root)
return true;
if(root.val > leftMax && root.val < rightMax) {
return helper(root.left,leftMax,root.val) && helper(root.right,root.val,rightMax);
}
return false;
}
Approach breakdown :-
Let's consider
helper(root,prev):-if(!root) return true;- If therootisundefinedwe can say that the BST is valid till now.if(root.val > leftMax && root.val < rightMax) { return helper(root.left,leftMax,root.val) && helper(root.right,root.val,rightMax); }- This is the core logic where we compareroot.valwithleftMaxandrightMax. Only ifroot.valis greater thanleftMaxandroot.valis less thanrightMax, we can proceed further to check for corresponding left subtree and right subtree and it's required that both of the subtrees need to returntruefor the BST to be valid. In case of left subtree,rightMaxwill change to currentroot.valand in case of right subtree,leftMaxwill change to currentroot.val.If the above condition fails, then we know it's not further required to check for any subsequent left or right subtree and simply return
false.
Inside
isValidBST, we doreturn helper(root,-Infinity,Infinity);and passleftMaxas-InfinityandrightMaxasInfinityas initial values for ourrootnode.
Out of all the approaches the last one is really clean and I guess an interviewer might expect it. I have given interviews where the first approach was enough and interviewer didn't ask for any optimizations. But if they do, I might skip the second one and jump straight to the third one.
Also I have ignored the space taken by call stack due to recursion and well you never know I might update this article in the future with more approaches if i feel so