As per MDN,

The repeat() method constructs and returns a new string which contains the specified number of copies of the string on which it was called, concatenated together.

Now one might think that there is a really straightforward to implement this. Yes there is but if asked in an interview and you go with the straightforward way, they will be like :-

How do I know this ?

Because I got mehhhhd......

So that's why we are going to see few approaches to solve it. The real optimized approach was not intuitive to me and is still something I am trying to wrap my head around. But I came up with a middle-ground approach that works better than the meh!! one.

And once, again we will take a synonym for repeat. Google time !!!!

replicate sounds cool.

Alright let's go implement String.prototype.replicate now :-

The Meh Approach

String.prototype.replicate = function(count) {
  let input = this;
  let result = "";
  for (let index = 0; index < count; index++) {
    result += input;
  }
  return result;
}

Meh explanation :- We initialize result to "" and start a for loop in which we iterate till count and simply keep appending the input to the result variable. Very straightforward but meh!!.

Meh benchmark :-

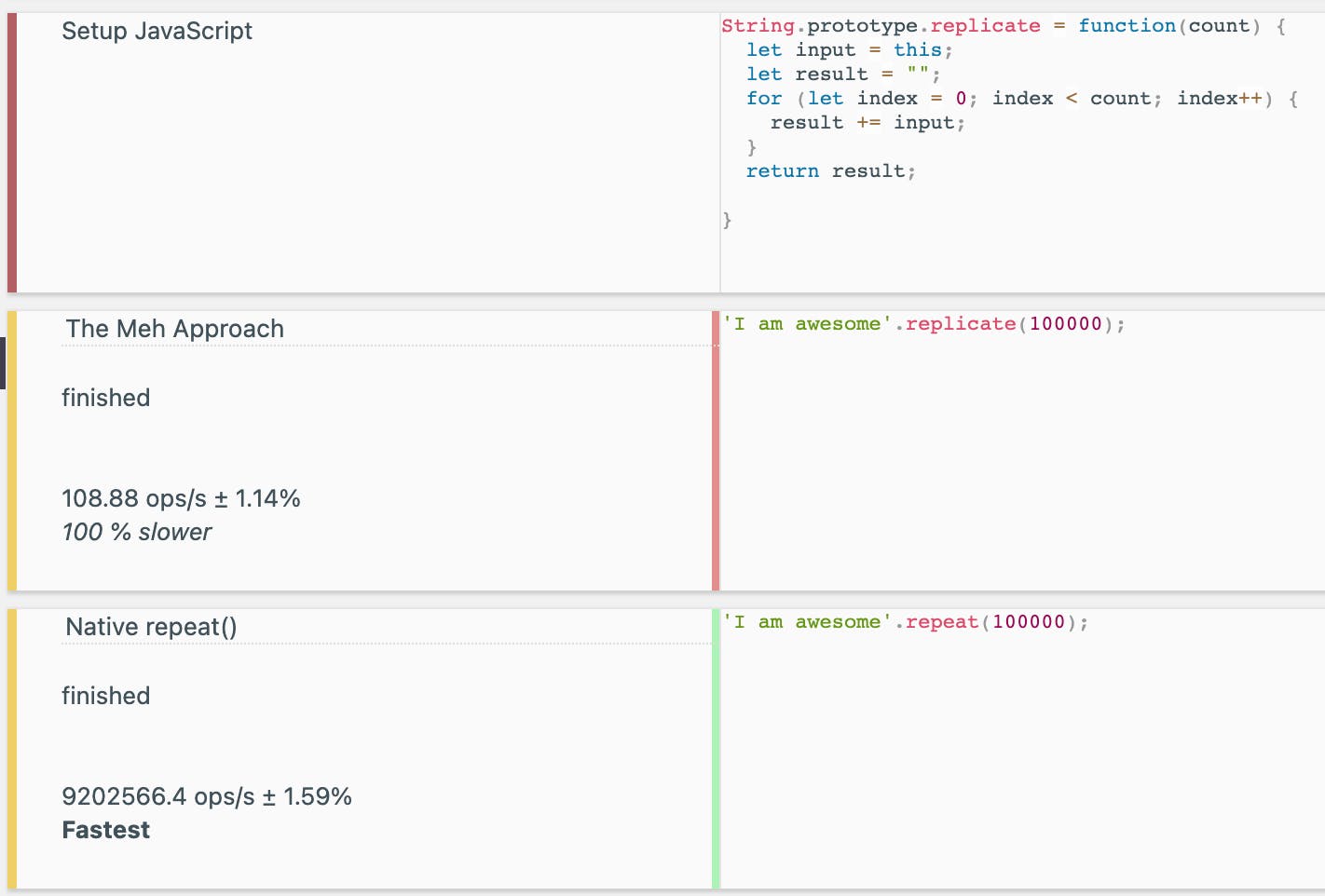
100 % slower with 108 operations per second compared to 9202566.4 operations per second . Let me cry in the corner.

The Little Less Meh Approach

String.prototype.replicate = function(count) {
  let input = this;
  let result = this.valueOf();
  for (var index = 2; index < count; index*=2) {
    result += result;
  }
  let remainingCount = count - index/2;
  return remainingCount > 0 ? result + input.replicate(remainingCount) : result;
}

Little Less Meh explanation :-

• Let's consider the case of 'hey'.replicate(10) :-
  • We have input initialized to this and result initialized to this.valueOf(). The valueOf() bit helps in decreasing the implicit conversion time that's happening whenever later result will be concatenated to itself.
  • Now the for loop stuff -
    • index is intialized to 2.
    • index should be less than count
    • index should be multiplied each time by 2
    • result will be appended to itself each time in the iteration:-
      • result for index = 2 will become heyhey
      • result for index = 4 will become heyheyheyhey
      • result for index = 8 will become heyheyheyheyheyheyheyhey
      • index will become 16 which is greater than 10 and we exit the loop.
    • remainingCount will be 10 - 16/2 = 2;
    • When remainingCount will be greater than 0, we will recurse by calling input.replicate(remainingCount) and add its result to current result or simply return result.

Little Less Meh benchmark :-

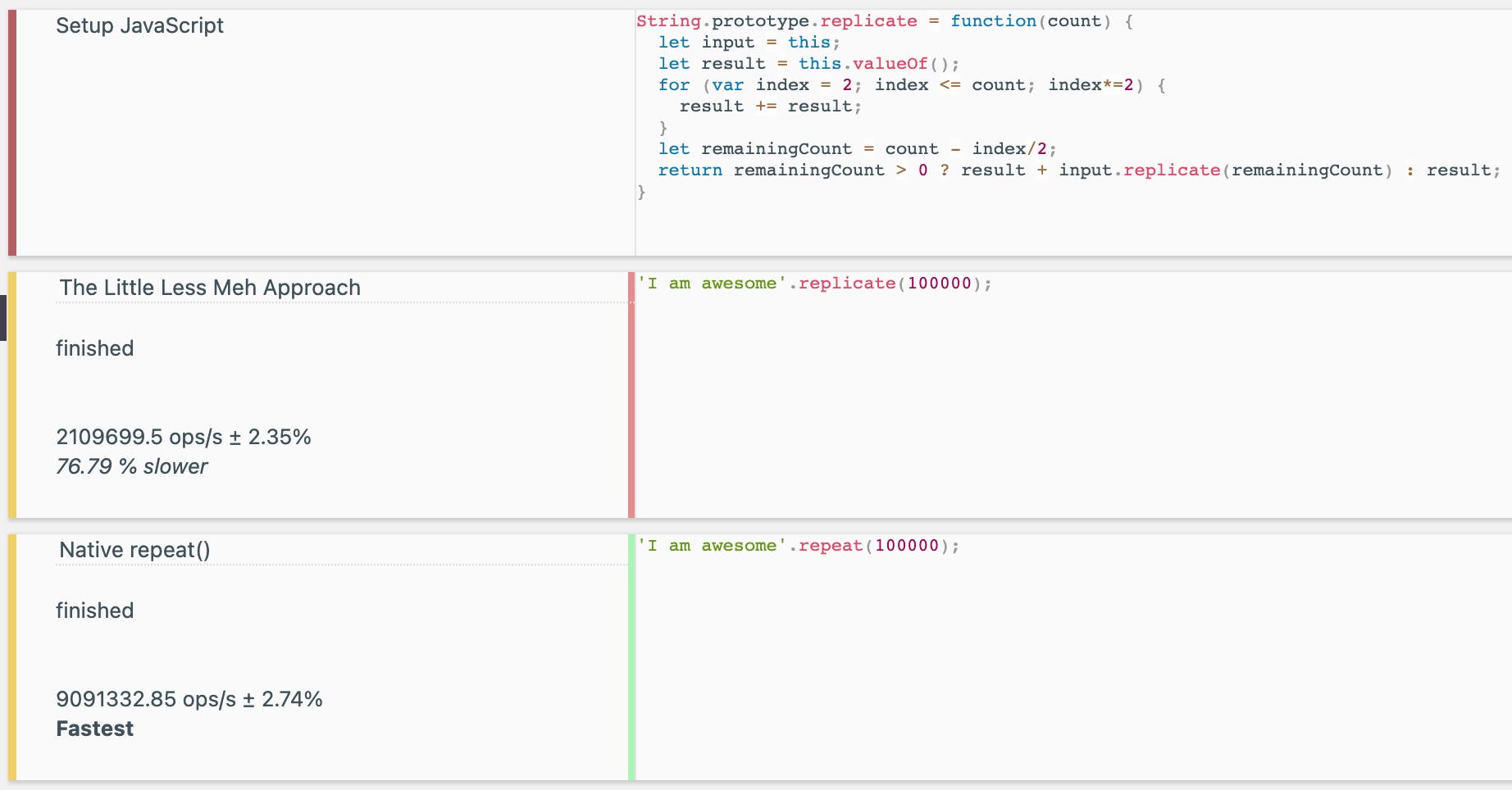
76.79% slower with 2109699.5 operations per second compared to 9091332.85 operations per second . That's still relatively slower than the native one but way way way faster than what we had initially.

Earlier performing the repetitions itself was O(count) but now the same is somewhere down the line of O(log(x)+log(y) +....+log(k)) but not completely O(log(count)).

In 'hey'.replicate(10) scenario :-

• First time, O(log(8)) work is done and then in next recursive step O(log(2)) i.e O(log(8) + log(2)). And if I am doing maths correct,

log(a) + log(b) = log(ab)

That means O(log(8) + log(2)) is O(log(16)) which is greater than O(log(10))(the optimal solution).

The legendary optimal solution I would have never landed upon without the internet

String.prototype.replicate = function(count) {
    let result = ''
    let pattern = this.valueOf();
    while (count > 0) {
        if (count & 1) 
            result += pattern;
        count >>= 1
        if (count) pattern += pattern;
    }
    return result;
};

Noob explanation :- I am still trying to understand the intuition behind this solution but I think it's to do with the fact that every number can be represented in a binary form. So let's say count is 5 then it can be represented as 101 in binary. So it's possible for us to repeat the string count times by just resorting to binary calculations. If we try to differentiate between 4 and 5, we know there is an extra 1 in latter case. Now instead of seeing the above code as some binary work of art, replace count&1 by count%2!==0 and count>>=1 by count=Math.floor(count/2). What this means is that, whenever count is odd, we would want to save the pattern till now in result variable. What is pattern ? pattern is repeated concatenation of itself similar to our earlier algorithm so it will always repeat in powers of 2. It's necessary to take care of the situation when count is not divisible by 2 and store the current pattern in result as we go until count becomes 0.

Did you expect a better explanation ? I can't give it right now since I am a noob in binary land. But maybe somewhere in a parallel universe I invented this Algo and helped Brendan Eich get rid of typeof null -> object 🤷‍♂️.

Best benchmark yet :-

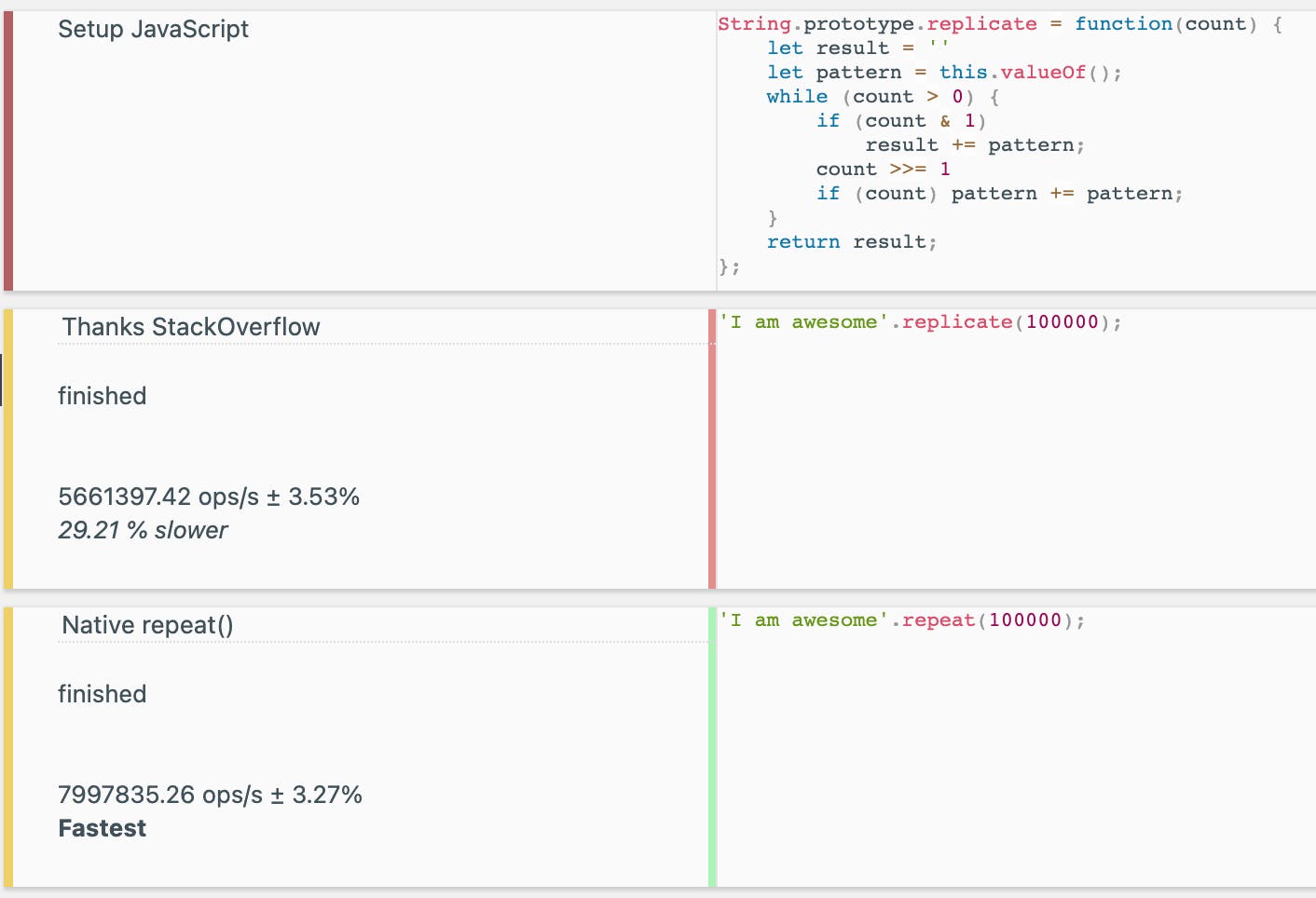
Still 29% slower ? WTH. But hey, I ain't competing with JavaScript engines here .

The Bonus MDN polyfill

 String.prototype.replicate = function(count) {
    var str = '' + this;
    count = +count;
    count = Math.floor(count);
    if (str.length == 0 || count == 0)
      return '';
    var maxCount = str.length * count;
    count = Math.floor(Math.log(count) / Math.log(2));
    while (count) {
       str += str;
       count--;
    }
    str += str.substring(0, maxCount - str.length);
    return str;
  }

Expected an explanation ? I don't care and you will see why 👇

The mandatory benchmark :-

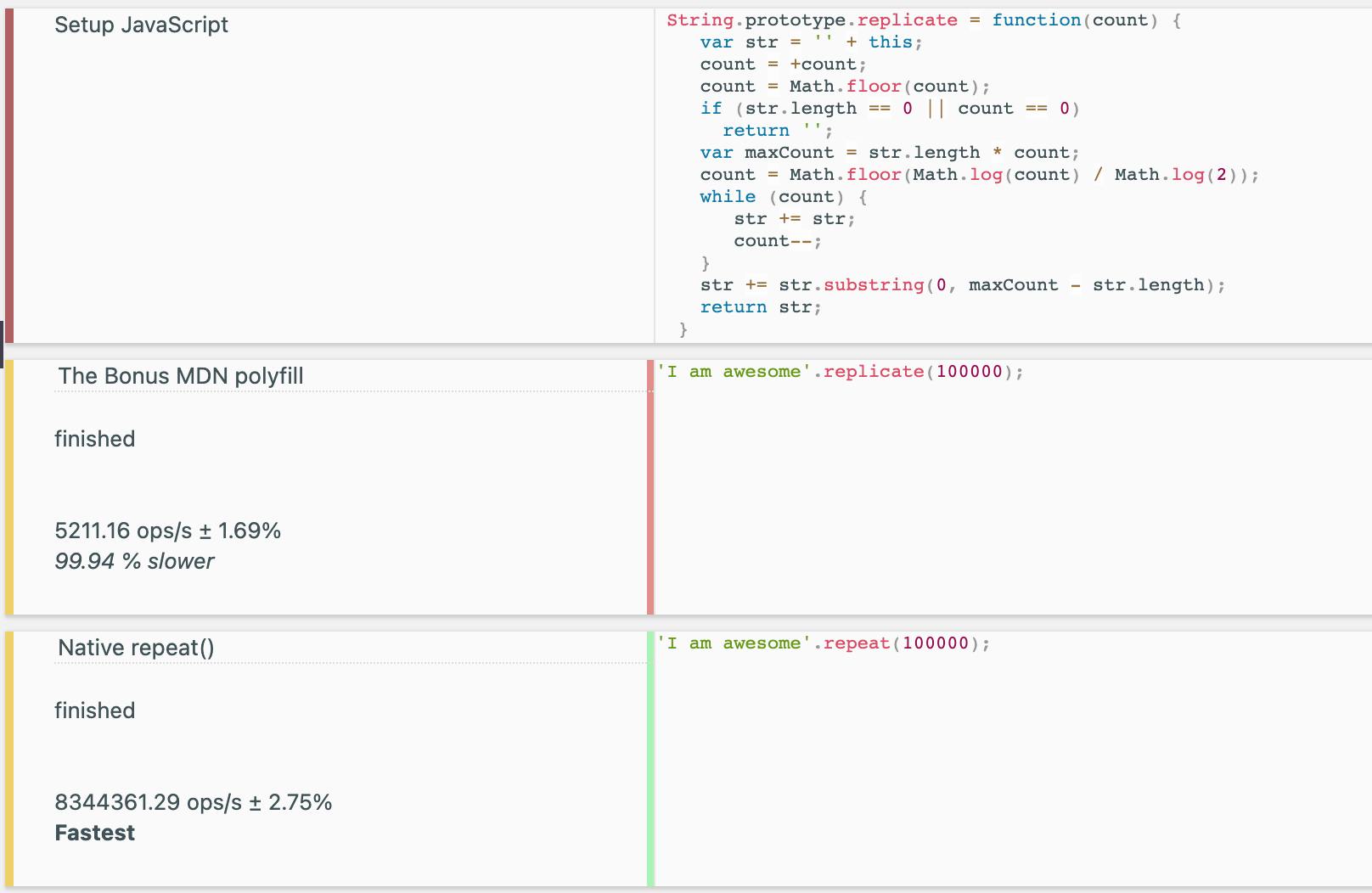
99.94 % slower with 5211.6 operations per second compared to 8344361.29 operations per second . And there is definite reason why it is even slower than what I came up with. What I think is happening is that upto a power of 2 which is less than count, we use the same ideology as in the optimal solution for concatenating and doubling length of str every time. But after that for the remaining length, it uses substring and appends that to str again. It's the second step of substring which makes it a costly operation. Though it does better than the initial Meh solution of 108 ops/s, it's still no where near around the best optimal solution I found online or even mine 😎.

MDN : 0 Lakshya : 1

JK. The site is and hopefully remains a gold mine ❤️.

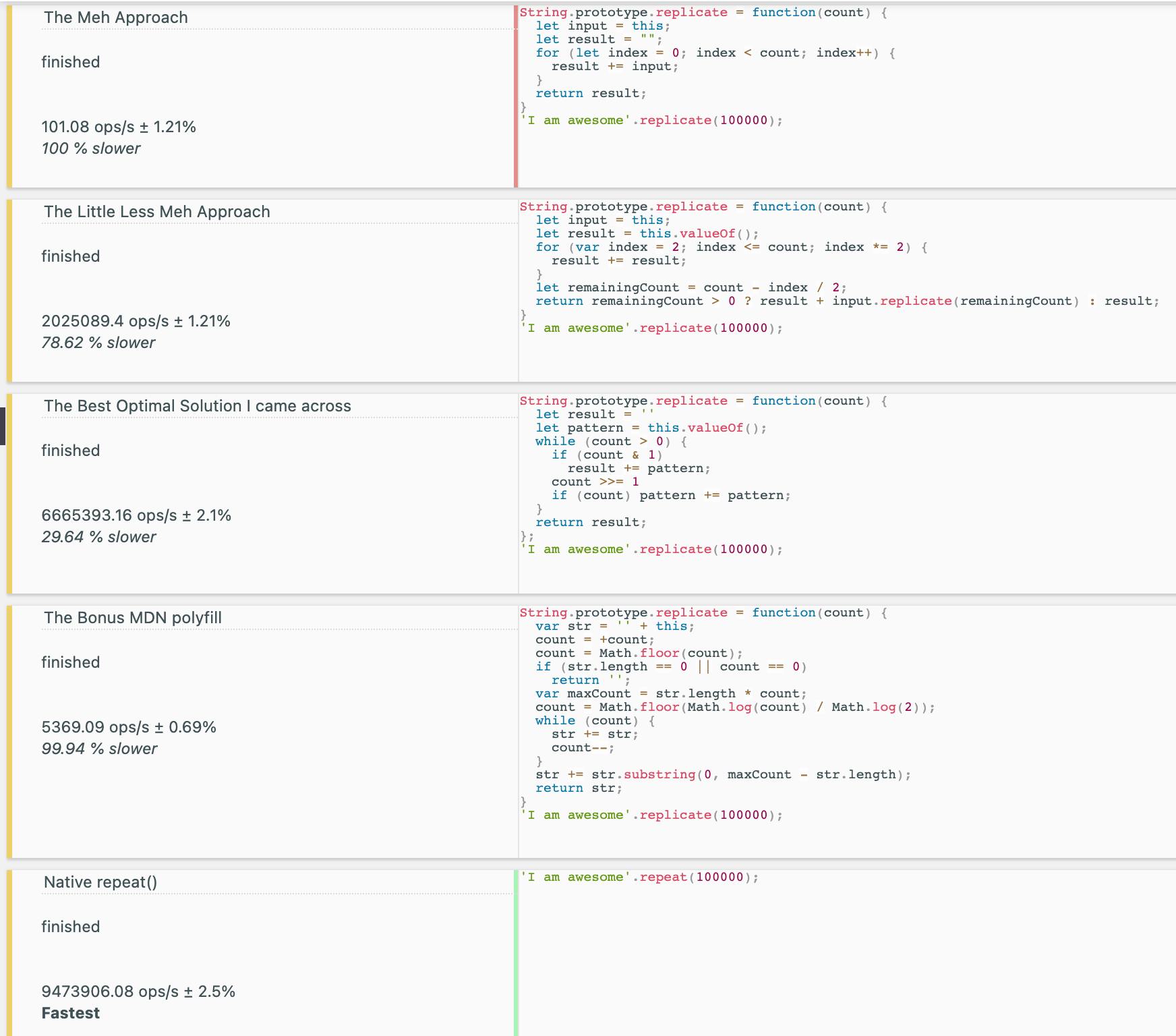
Here are the overall benchmarks :-

Have something to add on ? Feel free to

Thank you for your time :D